카테고리 없음

network communities

hgglife 2019. 10. 18. 22:25

중요 용어

Granovetter's theory

Edge betweeness

Granovetter's 이론에 따른 네트워크 모델은 클러스터링 된거에 몇몇 local bridge로 연결되있는 모양이다

 

중간 생략

Edge betweenness

노드사이에 그 경로를 지나서 연결된 갯수를 의미한다

SCC bridge scc 일때  SCC*SCC 가 Edge betweeness가 되며

이때 bridge edge가 아닐경우 그 갯수로 나누어 주면된다

 

그리고 다이아몬드처럼해서 바꿔서 노드갯수 구하는게있고

 

모듈레이션 Q 구하기

노드끼리   tightly하게 연결되있는걸 커뮤니티라고하는데

모듈러리티 Q는 이때 네트워크를 몇개의 파티션으로 나눠야하는가에대한 질문이다

 

파티션그룹 s 가 전체 네트워크  S안에 있다고할때

Q =  원래 그룹s의  edge 갯수 - 현재 모델에서 Edge개수만 같게해서 재조합한모델   s의 예상  edge 개수

새로만든 s는 전이랑 총 edge  개수는 같지만  무작위로 연결된다

노드사이에 예상되는  Edge의개수 i노드와 j노드의갯수를  k(i) and K(j)로 표현

k(i)*k(j) / 2m

m은 노드 전체의 개수

Q = 1/2m 시그마(s->S)시그마(i->s) 시그마(j->s)(A(ij) - k(i)k(j)/2m) 인데

이설명은 조금 어렵다 그래서 다른설명을 찾아봤는데

모듈레이션 Q 구하기

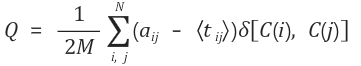
Q    =  모듈성

M =  전체링크수

N = 전체노드수

a(ij) = i  와 j 간의 링크 (있을때 1 없을때 0)

t(ij) = 무작위로 재연결 하였을때 i와 j 의 링크

<t(ij)> 무작위로 재연결했을때 t(ij)의 기대치

c(i)  =  i 노드가 속하는 커뮤니티

δ(C(i), C(j))  C(i)와 C(j)가 같은 커뮤니티일 때 1, 다를 때 0

이때 우리가 <t(ij) >를 어떻게 구할수있는지에 대한 의문이 생길것이다

M     전체 링크 수  

p_i    링크 중 한 쪽 끝에 노드 i가 있을 확률

그렇다면 p(i) 는 어떻게 구할것인가 매우 큰 고민에 빠지게 될수있는데

k_i     노드 i가 지니는 링크의 개수

M      전체 링크 수  

로 표현할수 있다 그렇기에 이식을 조금 변형하면

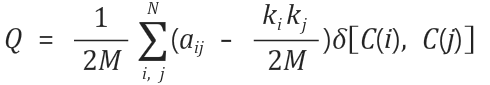
우리말로쓰자면

모듈러리티Q 의값은 1/2전체링크수 * (aij의링크 -  i의노드수*j의 노드수/2전체링크수)*δ(C(i), C(j))(1->N)

여기서 하나더 의문점이 생기는데 같은 커뮤니티인지 어떻게 구별할것인가

그래서 이 식을 커뮤니티 관점에서 바라보는 식으로 변형한다. 윗 식에서 δ함수는 커뮤니티가 같을 때만 1이 되므로, 커뮤니티 관점에서 식을 정리하여 δ함수를 없앨 수 있다.

 

 

l              커뮤니티 넘버

n_C          전체 커뮤니티의 개수  

이렇게 모듈러리티를 계산하여서  모듈러리티가 가장클때까지만 나누고

이후에는 클러스터를 나누지 않으면 된다 .

솔찍하게 이해 완벽하게 안됬는데 커뮤니티개수가 증가하면 모듈러리티가 감소하는건가?

어렵다 어려워

 

모듈러리티 자료출처 - https://mons1220.tistory.com/93